黎曼zeta函数的奥秘剖析素数分布的秘密

黎曼zeta函数到底是什么

嘿，咱们先聊聊黎曼zeta函数到底是啥？简单来说，它是个超级重要的数学函数，尤其在复分析和数论里地位杠杠的。你知道吗，它跟“素数”的分布紧密相关。

这个函数最初定义为一个无穷级数，形式就是 ζ(s) = ∑_{n=1}^∞ 1/n^s，s是个复数，当实部大于1时，这个级数才收敛，没错，就是这么“娇气”。
随着数学家们的钻研，黎曼把它定义扩大到更宽广的复数区域，这过程叫做“解析延拓”，简单讲就是让函数“变身”在更大范围内依旧能正常用。
有趣的是，它还能写成一个跟素数紧密相关的欧拉乘积公式，像个密码一样把素数和函数联系起来，简直酷炸了！

而且，黎曼zeta函数在物理学、统计学等领域也常被提起，真是个多面手。

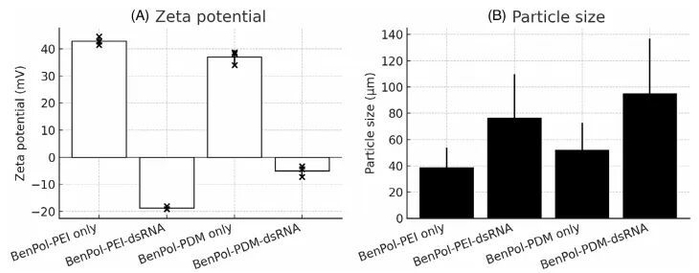
黎曼zeta函数是怎么帮助我们理解素数分布的呢

说到素数，这玩意儿简单说，是只能被1和自身整除的神奇数字，比如2、3、5、7……可它们的分布超复杂，没个明显规律，搞得数学家很头疼。

黎曼通过zeta函数把素数的秘密藏了进去，让咱们可以用复分析这些高级工具去“窥探”素数分布。
有个超级重要的概念叫黎曼假设，简单来说就是方程ζ(s) = 0的非平凡零点，全都得在线上D的一个特别位置，这被认为是理解素数乱中有序的关键。
除了这些，黎曼假设和zeta函数的零点还被证明跟素数定理有关，素数定理简单理解就是说，素数的分布随着数变大，规律开始浮现，速度和什么有关好像也能通过zeta函数“测”出来。

总的来说，黎曼zeta函数就像个桥梁，把纯数学的“素数”世界和复变分析的“函数”世界连起来，可不得不佩服当年这哥们牛逼！

相关问题解答

黎曼zeta函数为什么只在实部大于1时级数收敛？

哎呀，这其实是因为当s的实部小于等于1时，那个无穷级数的项不够“乖”，总得往下加，根本停不下来，就没法算出个具体数字了。咱们可以想象成，数列的“和”跑去无穷大了，没法用。好在有了“解析延拓”，数学家们搞出花样，在更大范围内给它开了路，让函数还能“正常运转”，这真的超厉害！

黎曼假设和素数分布到底有什么关系？

这个问题棒！简单说，黎曼假设就像个超级厉害的魔法钥匙，告诉我们zeta函数的零点都躺在那个“魔法线”上。如果这个猜测正确，那么素数的分布就会特别“规整”，不像现在看起来那么乱七八糟。换句话说，它帮咱们预测素数“间距”的规律性，也许还能让未来的密码学更安全或者破解更高效，超级吸引人吧！

黎曼zeta函数跟Gamma函数有啥关联？

哈，这两个函数其实像“好基友”一样互帮互助。特定情况下，黎曼zeta函数的解析延拓需要借助Gamma函数的积分定义来完成。Gamma函数就好比是那个“万能胶”，帮着连接和塑造zeta函数的解析性质，这样zeta函数才能在更大需要的复数域内“活跃”，说白了，就是Gamma函数让zeta函数更灵活、更完美。

解析延拓到底是啥，能不能再通俗点？

好的，解析延拓就像给一个有限功能的工具升级，原本只能用在某个范围内，可升级后它能用得更宽更广。就拿zeta函数来说，最开始它只能在实部大于1的地方“工作”，但是数学家通过高级技巧，让它在复平面上的绝大多数地方“也能工作”。这就像把一个限定版游戏变成了完整版，得用到一些特别牛逼的积分公式和复变函数理论，是不是超级酷？

本文来自作者[关炫杰]投稿，不代表跃庆号立场，如若转载，请注明出处：https://www.mingcaifu.com/zhishi/202512-P6QRbCJ10y.html