勾股定理是如何引发第一次数学危机的?
勾股定理引发的第一次数学危机,主要是因为它暴露出了一个大秘密——无理数的存在。这可是当时毕达哥拉斯学派的信仰大忌,他们坚信“万物都可以用整数或者整数之比表示”,也就是有理数。可是,勾股定理告诉我们,在一个直角三角形里,直角边的平方和等于斜边的平方,这一发现让他们震惊,因为斜边的长度竟然不能用简单的整数比来表达,这直接颠覆了他们的世界观,数学界也因此陷入了深深的困惑。

数学史上的三次危机到底是什么?勾股定理又扮演了怎样的角色?
-
第一次数学危机:发生在公元前5世纪,毕达哥拉斯学派深信“万物皆数”,就是说所有长度都能用有理数表达。可是,学派成员希伯索斯根据勾股定理发现,边长为1的正方形对角线的长度既不是整数,也不是整数的比,这就是著名的√2。这个发现被当时人视为“荒谬”,因为它违背了毕达哥拉斯学派的信条,对希腊数学家们的传统认知产生了极大冲击。
-
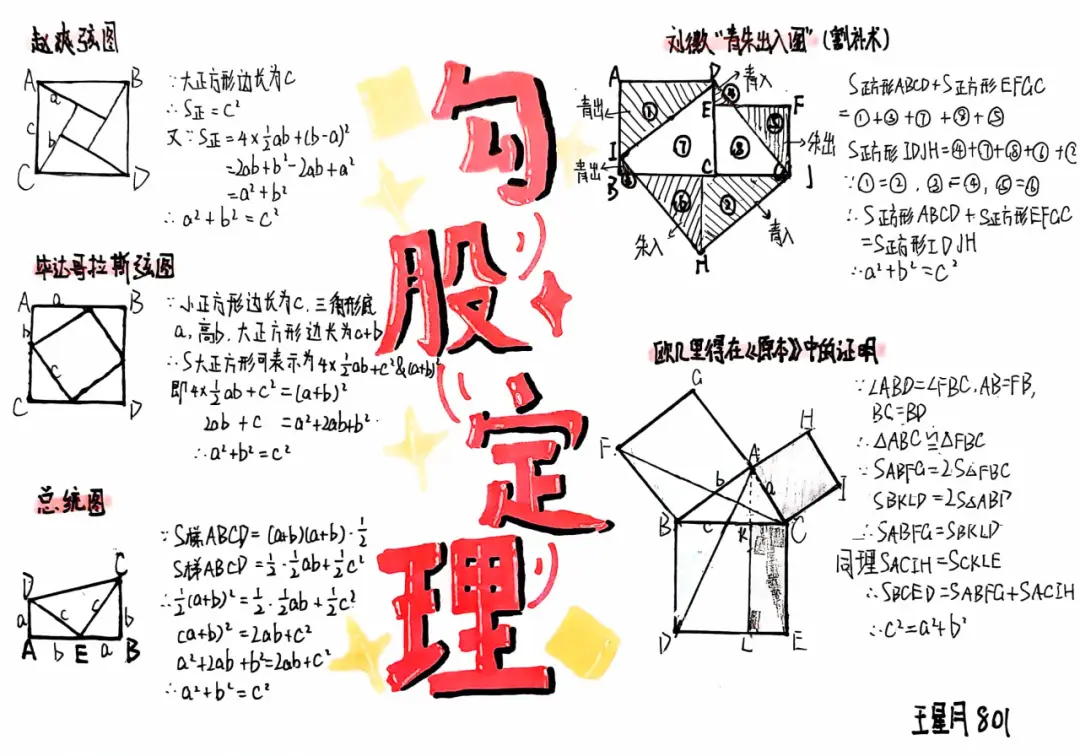
勾股定理的历史意义:勾股定理不仅揭示了数与量的区别,还推动了数学从简单的计算和测量转向严密的证明和逻辑推理。多样的证明方法和它在不定方程中的应用,都让它成为数学发展的里程碑。它的发现和研究,催生了首次数学危机,也为数学科学奠定了坚实基础。
-
数学的三大危机总结:第一次危机是无理数的出现,挑战了“万物皆数”的信念;后续的危机则围绕数学基础和逻辑体系展开,都是数学发展过程中不可避免的“成长烦恼”。勾股定理在这里起了非常关键的启蒙作用,提醒我们数学的世界比想象中更丰富也更复杂。
相关问题解答
-
为什么勾股定理会导致数学危机?
哇,这个其实挺酷的。勾股定理本来是解决直角三角形边长关系的简单定理,但它暴露了一个大问题,就是有些长度根本没法用整数或者分数来表示,像√2就是一个典型的无理数。这跟毕达哥拉斯学派“万物都是整数或分数”的信念直接冲突,所以就引发了数学界的第一次大震动,大家都懵了,觉得数学是不是要重写了! -
毕达哥拉斯学派为什么那么看重“万物皆数”?
其实他们觉得宇宙一切都能用数字来解释,特别是整数和分数,这让世界看起来非常有秩序又简单。可结果发现,有些数根本写不成分数,完全打破了他们的理想世界,太不可思议了!这就像你认为世界是黑白的,突然发现彩虹一样,震撼到不行。 -
无理数到底是什么?为什么它们这么特别?
简单来说,无理数就是那些不能用两个整数的比表示的数,比如√2、π等。它们特别的是,不能用简单的分数表达,数字小数部分无限不循环,超级复杂。正是这些“怪异”的数字让数学变得更丰富,也让我们理解了数字世界的多样性。 -
勾股定理的发现对现代数学有什么影响?
哎呀,影响大得不得了!勾股定理推动数学从计算工具变成了严密的证明科学,也开启了对无理数和数论的深入研究,还影响了几何、代数甚至物理学的发展。可以说,没有勾股定理,现代数学可能会慢很多,真的是数学界的“开山鼻祖”之一!
本文来自作者[单于仲智]投稿,不代表跃庆号立场,如若转载,请注明出处:https://www.mingcaifu.com/zlan/202510-mErstDhIOGH.html






评论列表(3条)
我是跃庆号的签约作者“单于仲智”
本文概览:勾股定理是如何引发第一次数学危机的? 勾股定理引发的第一次数学危机,主要是因为它暴露出了一个大秘密——无理数的存在。这可是当时毕达哥拉斯学派的信仰大忌,他们坚信“万物都可以用整...
文章不错《勾股定理为什么会引发数学史上的大危机?》内容很有帮助